Подбор сменных зубчатых колес. Программа для подбора

ПОРЯДОК ПОЛЬЗОВАНИЯ ТАБЛИЦАМИ / ПРОГРАММОЙ

Для подбора сменных колес искомое передаточное отношение выражается в виде десятичной дроби с числом знаков соответственно требуемой точности. В «Основных таблицах» для подбора зубчатых колес (стр. 16—400) находим колонку с заголовком, содержащим первые три цифры передаточного отношения; по остальным цифрам находим строку, на которой указаны числа зубьев ведущих и ведомых колес.

Пример.

Требуется подобрать сменные колеса гитары для передаточного отношения 0,2475586. Сначала находим колонку с заголовком 0,247—0000, а под ним ближайшее значение к последующим десятичным знакам искомого передаточного отношения (5586). В таблице находим число 5595, соответствующее набору сменных колес (23*43) : (47*85). Окончательно получаем:

i = (23*43)/(47*85) = 0,2475595. (1)

Относительная погрешность сравнительно с заданным передаточным отношением :

δ = (0,2475595 — 0,2475586) : 0,247 = 0,0000037.

Строго подчеркиваем: во избежание влияния возможной опечатки нужно обязательно проверить полученное соотношение (1) на калькуляторе. В тех случаях, когда передаточное отношение больше единицы, необходимо выразить его обратную величину в виде десятичной дроби, по найденному значению в таблицах отыскать числа зубьев ведущих и ведомых сменных колес и поменять ведущие и ведомые колеса местами.

Пример.

Требуется подобрать сменные колеса гитары для передаточного отношения i = 1,602225. Находим обратную величину 1:i = 0,6241327. В таблицах для ближайшего значения 0,6241218 находим набор сменных колес: (41*65) : (61*70). Учитывая, что решение найдено для обратной величины передаточного отношения, меняем местами ведущие и ведомые колеса:

i = (61*70)/(41*65) = 1,602251

Относительная погрешность подбора

δ = (1,602251 — 1,602225) : 1,602 = 0,000016.

Обычно требуется подбирать колеса для передаточных отношений, выраженных с точностью до шестого, пятого, а в отдельных случаях и до четвертого десятичного знака. Тогда семизначные числа, приведенные в таблицах, можно округлять с точностью до соответствующего десятичного знака. Если имеющийся комплект колес отличается от нормального (см. стр. 15), то, например, при настройке цепей дифференциала или обкатки можно выбрать подходящую комбинацию из ряда соседних значений с погрешностью, удовлетворяющей условиям, изложенным на стр. 7—9. При этом некоторые числа зубьев можно заменять. Так, если число зубьев комплекта не свыше 80, то

(58*65)/(59*95) = (58*13)/(59*19) = (58*52)/(59*76)

«пятковую» комбинацию предварительно преобразуют так:

(25*90)/(70*85) = (5*9)/(7*17)

а затем, по полученным множителям подбирают числа зубьев.

ОПРЕДЕЛЕНИЕ ДОПУСТИМОЙ ПОГРЕШНОСТИ НАСТРОЙКИ

Очень важно различать абсолютную и относительную погрешности настройки. Абсолютной погрешностью называют разность между полученным и требуемым передаточными отношениями. Например, требуется иметь передаточное число i = 0,62546, а получено i = 0,62542; абсолютная погрешность будет 0,00004. Относительной погрешностью называют отношение абсолютной погрешности к требуемому передаточному числу. В нашем случае относительная погрешность

δ = 0.00004/0,62546 = 0,000065

Следует подчеркнуть необходимость суждения о точности настройки по относительной погрешности.

Общее правило.

Если какая-либо величина А, получаемая настройкой через данную кинематическую цепь, пропорциональна передаточному отношению i, то при относительной погрешности настройки δ абсолютная погрешность будет Аδ.

Например, если относительная погрешность передаточного отношения δ =0,0001, то при нарезании винта с шагом t отклонение в шаге, зависящее от настройки, будет 0,0001 * t. Та же относительная погрешность при настройке дифференциала зубофрезерного станка даст дополнительное вращение заготовки не на требуемую дугу L, а на дугу с отклонением 0,0001 * L.

Если указан допуск на изделие, то абсолютное отклонение размера вследствие неточности настройки должно составлять только некоторую долю этого допуска. В случае более сложной зависимости какой-либо величины от передаточного отношения полезно прибегать к замене фактических отклонений их дифференциалами.

Настройка цепи дифференциала при обработке винтовых изделий.

Типичной является следующая формула:

i = c*sinβ/(m*n)

где с — постоянная цепи;

β — угол наклона винтовой линии;

m — модуль;

n — число заходов фрезы.

Продифференцировав обе части равенства, получим абсолютную погрешность di передаточного отношения

di = (c*cosβ/m*n)dβ

тогда допустимая относительная погрешность настройки

δ = di/i = dβ/tgβ

Если допустимое отклонение угла винтовой линии dβ выразить не в радианах, а в минутах, то получим

δ = dβ/3440*tgβ (3)

Например, если угол наклона винтовой линии изделия β = 18°, а допустимое отклонение в направлении зуба dβ = 4" = 0',067, то допустимая относительная погрешность настройки

δ = 0,067/3440*tg18 = 0,00006

Наоборот, зная относительную погрешность взятого передаточного отношения, можно по формуле (3) определить допущенную погрешность в угле винтовой линии в минутах. При установлении допустимой относительной погрешности можно в подобных случаях пользоваться тригонометрическими таблицами. Так, в формуле (2) передаточное отношение пропорционально sin β. По тригонометрическим таблицам для взятого числового примера видно, что sin 18° = 0,30902, а разность синусов на 1' составляет 0,00028. Следовательно, относительная погрешность на 1' составляет 0,00028 : 0,30902 = 0,0009. Допустимое отклонение винтовой линии — 0,067, поэтому допустимая погрешность передаточного отношения 0,0009*0,067 = 0,00006, такая же, как и при расчете по формуле (3). Когда оба сопряженных колеса нарезаются на одном станке и по одной настройке цепи дифференциала, то погрешности в направлении линий зубьев допускаются значительно большие, так как у обоих колес отклонения одинаковы и незначительно влияют только на боковой зазор при зацеплении сопряженных колес.

Настройка цепи обкатки при обработке конических колес.

В этом случае формулы настройки выглядят так:

i = p*sinφ/z*cosу или i = z/p*sinφ

где z — число зубьев заготовки;

р — постоянная цепи обкатки;

φ — угол начального конуса;

у — угол ножки зуба.

Пропорциональным передаточному отношению оказывается радиус основной окружности. Исходя из этого, можно установить допустимую относительную погрешность настройки

δ = (Δα)*tgα/3440

где α — угол зацепления;

Δα — допустимое отклонение угла зацепления в минутах.

Настройка при обработке винтовых изделий.

Формула настройки

δ = Δt/t или δ = ΔL/1000

где Δt — отклонение в шаге винта за счет настройки;

ΔL — накопленная погрешность в мм на 1000 мм длины резьбы.

Величина Δt дает абсолютную ошибку шага, а величина ΔL характеризует по существу относительную погрешность.

Настройка с учетом деформации винтов после обработки.

При нарезании метчиков с учетом усадки стали после последующей термической обработки или с учетом деформации винта вследствие нагревания при механической обработке, процент усадки или расширения непосредственно указывает на необходимое относительное отклонение в передаточном отношении сравнительно с тем, какое получилось бы без учета этих факторов. В этом случае относительное отклонение передаточного отношения в плюс или минус является уже не ошибкой, а преднамеренным отклонением.

Настройка делительных цепей. Типичная формула настройки

i = p/z

где р — постоянная;

z — число зубьев или других делений на один оборот заготовки.

Нормальный комплект из 35 колес обеспечивает абсолютно точную настройку до 100 делений, так как в числах зубьев колес содержатся все простые множители до 100. В такой настройке погрешность вообще недопустима, так как она равна:

Δl= пD*B*δ/s

где Δl — отклонение линии зуба на ширине заготовки В в мм;

пD — длина начальной окружности или соответствующей другой окружности изделия в мм;

s — подача вдоль оси заготовки на один ее оборот в мм.

Только в грубых случаях эта погрешность может не играть роли.

Настройка зубофрезерных станков при отсутствии требуемых множителей в числах зубьев сменных колес.

В таких случаях (например, при z = 127) можно настроить гитару деления приближенно на дробное число зубьев, а необходимую поправку произвести, используя дифференциал [5]. Обычно формулы настройки гитар деления, подач и дифференциала выглядят так:

x = pa/z ; y = ks ; φ = c*sinβ/ma

Здесь р, k, с — соответственно постоянные коэффициенты этих цепей; а — число заходов фрезы (обычно а = 1).

Настраиваем указанные гитары согласно формулам

x = paA/Az+-1 ; y = ks ; φ' = пc/asA

где z — число зубьев обрабатываемого колеса;

А — произвольное целое число, выбираемое так, чтобы числитель и знаменатель передаточного отношения разлагались на множители, подходящие для подбора сменных колес.

Знак (+) или (—) также выбирается произвольно, что облегчает разложение на множители. При работе правой фрезой, если выбран знак (+), промежуточные колеса на гитарах ставятся так, как это делают согласно руководству по работе на данном станке для правовинтовой заготовки; если выбран знак (—), промежуточные колеса ставят, как для левовинтовой заготовки; при работе левой фрезой — наоборот.

Желательно выбирать А в пределах

(1/2)*(пc/as) < A < 4*(пc/as)

тогда передаточное отношение цепи дифференциала будет от 0,25 до 2.

Особо необходимо подчеркнуть, что при взятых сменных колесах на гитару подач фактическая подача должна быть определена для подстановки в формулу настройки дифференциала с большой точностью. Лучше рассчитать ее по кинематической схеме станка, так как постоянный коэффициент k в формуле настройки подач в руководстве к станку иногда дается приближенно. При несоблюдении этого указания зубья колеса могут вместо прямых получиться заметно скошенными.

Рассчитав подачу, практически получают по первым двум формулам (4) точную настройку. Тогда допустимая относительная погрешность в настройке гитары дифференциала

δ = sA*Δl/пmb (5)

де b — ширина зубчатого венца заготовки;

Δl — допустимое отклонение направления зуба на ширине венца в мм.

В случае нарезания колес с винтовыми зубьями нужно с помощью дифференциала сообщить фрезе дополнительное вращение для образования винтовой линии и дополнительное вращение для компенсации разности между требуемым числом делений и фактически настраиваемым числом делений. Получаются формулы настройки:

x = paA/Az+-1 ; y = ks ; φ" = c*sinβ/ma +- пc/asA

В формуле для x знак (+) или (—) выбирается произвольно. В этих случаях:

1) если направление винта у фрезы и заготовки одинаковое в формуле для φ" принимают тот же знак, какой выбран в формуле для х;

2) если направление винта у фрезы и заготовки разное, то в формуле для φ" принимают знак, обратный выбранному для х.

Промежуточные колеса на гитарах расставляют, как указано в инструкции к данному станку, согласно направлению винтовых зубьев. Только в случае, если окажется, что φ" < 0, поступают наоборот. Погрешность можно оценивать по формуле (5). В случае необходимости нетрудно аналогичным путем получить настройки для нарезания червячных колес, как в случае радиальной, так и в случае осевой подачи фрезы.

Бездифференциальная настройка.

В ряде случаев при обработке винтовых изделий можно использовать более жесткие бездифференциальные станки, если не требуется вторичного прохода обрабатываемых впадин с той же установки и при точном попадании во впадину. Если наладка станка производится при заранее определенной подаче, обусловленной малым числом сменных колес или наличием коробки подач, то настройка цепи деления требует большой точности, т. е. она должна производиться как прецизионная. Допустимая относительная погрешность

δ = Δβ*s/(10800*D*cosβ*cosβ)

где Δβ — отклонение винтовой линии изделия в минутах;

D — диаметр начальной окружности (или цилиндра) в мм;

β — угол наклона зуба заготовки к ее оси;

s — подача на один оборот заготовки вдоль ее оси в мм.

Чтобы избежать трудоемкой прецизионной настройки, поступают следующим образом. Если для гитары подач можно использовать достаточно большой комплект колес (25 и более, в частности нормальный комплект и таблицы данной книги), то сначала считают заданную подачу s ориентировочной. Настроив цепь деления и считая настройку вполне точной, определяют, какой для этого должна быть осевая подача s'.

Обычную формулу цепи деления переписывают так:

x = (p/z)*(T/T+-z') = ab/cd (6)

где р — постоянный коэффициент цепи деления;

z — число делений изделия (зубьев, канавок);

T = пmz/sinβ - шаг винтовой линии заготовки в мм (он может быть определен и другим путем);

s' — подача инструмента вдоль оси заготовки на один оборот в мм. Знак (+) принимают при разных направлениях винта фрезы и заготовки; знак (—) при одинаковых.

Подобрав, в частности по таблицам данной книги, ведущие колеса с числами зубьев а и b, а ведомые — с и d, из формулы (6) определяем точно требуемую подачу

s' = T(pcd - zab)/zab (7)

Подставляем значение s' в формулу настройки подач

y = ks' (8)

Относительная погрешность δ настройки подачи вызывает соответствующую относительную погрешность шага T винтовой линии. На основании этого нетрудно установить, что при настройке гитары подач можно допустить относительную погрешность

δ = Δβ/3440*tgβ (9)

Из сравнения этой формулы с формулой (3) видно, что допустимая в этом случае погрешность настройки гитары подач такая же, какой она является при обычной настройке цепи дифференциала. Следует еще раз подчеркнуть необходимость знания точного значения коэффициента k в формуле подач (8). Если есть сомнения, лучше проверить его расчетом по кинематической схеме станка. Если сам коэффициент k определен с относительной погрешностью δ, то это вызывает дополнительное отклонение винтовой линии на Δβ, определяемое при данном β из соотношения (9).

УСЛОВИЯ СЦЕПЛЯЕМОСТИ СМЕННЫХ КОЛЕС

В руководствах к станкам полезно давать графики, по которым легко заранее оценить возможность сцепляемости данной комбинации колес. На рис. 1 показаны два крайних положения гитары, определяемые круговыми пазами В. На рис. 2 приведен график, на котором дуги окружностей проведены из точек Oc и Od, являющихся центрами первого ведущего колеса а и последнего ведомого колеса d (рис. 3). Радиусы этих дуг в принятом масштабе равны расстояниям между центрами сцепляющихся между собой сменных колес с суммами чисел зубьев 40, 50, 60 и т. д. Эти суммы чисел зубьев для первой пары сцепляющихся колес а + с и второй пары b + d проставлены у концов соответствующих дуг.

Пусть по таблицам найден набор колес (50*47) : (53*70). Сцепятся ли они в порядке 50/70 * 47/53 ? Сумма чисел зубьев первой пары 50 + 70 = 120 Центр пальца должен лежать где-то на дуге с пометкой 120, проведенной из центра Oa. Сумма чисел зубьев колес второй пары 47 + 53 = 100. Центр пальца должен быть на дуге с пометкой 100, проведенной из центра Od. В итоге центр пальца установится в точке с на пересечении дуг. Согласно схеме сцепление колес возможно.

Для комбинации 30/40 * 20/50 сумма чисел зубьев первой пары 70, второй также 70. Дуги с такими пометками не пересекаются внутри фигуры, следовательно, сцепление колес невозможно.

Рекомендации конструктору гитары.

Кроме графика, приведенного на рис. 2, желательно вычертить также контур коробки и другие детали, которые могут мешать установке зубчатых колес на гитару. Для наилучшего использования таблиц данной книги конструктору гитары целесообразно соблюдать следующие условия, которые не являются строго обязательными, но желательными:

1. Расстояние между постоянными ОСЯМИ Oa И Od должно быть таким, чтобы две пары колес с общей суммой зубьев 180 могли еще входить во взаимное зацепление. Наиболее желательное расстояние Oa — Od составляет от 75 до 90 модулей.

2. На первом ведущем валике должно устанавливаться колесо с числом зубьев хотя бы до 70, на последнем ведомом — до 100 (если по габаритам допустимо, можно предусмотреть до 120—127 для некоторых случаев уточненных настроек).

3. Длина прорези гитары при крайнем положении пальца должна обеспечивать сцепляемость колес, расположенных на пальце и на оси гитары с суммой зубьев не менее 170—180.

4. Крайний угол отклонения паза гитары от прямой, соединяющей центры Oa и Od, должен быть не менее 75—80°.

5. Коробка должна иметь достаточные габариты. Сцепляемость наиболее неблагоприятных комбинаций должна быть проверена по графику, прилагаемому в руководстве к станку (см. рис. 2).

Рекомендации настройщику.

Настройщик станка или механизма должен использовать данный в руководстве график (см. рис. 2), но, кроме того, учитывать, что чем больше зубчатое колесо на первом ведущем валу (при данном моменте сил), тем меньше усилие на зубьях первой пары; чем больше колесо на последнем ведомом валу, тем меньше усилие на зубьях второй пары.

Рассмотрим замедляющие передачи, т. е. случай, когда i<1. Обозначим числа зубьев ведущих колес z1 и z2, при этом z1 < z2; числа зубьев ведомых колес Z3 и z4, при этом Z3 < Z4 Из изложенного следует, что числа зубьев ведомых колес всегда надо брать в таком порядке, как они указаны в таблицах. Числа зубьев ведущих колес можно брать и в прямом, и в обратном порядке. Следовательно, остается выбирать одну из двух комбинаций

z1/z3 * z2/z4 ; z2/z3 * z1/z4 (10)

Предпочтительнее вторая комбинация. Она обеспечивает меньший момент сил на промежуточном валу и позволяет соблюсти предъявляемые дополнительные условия (см. рис. 3):

а+с > b+(20...25); b + d > с+(20...25) (11)

Эти условия ставятся для предотвращения упора сменных колес в соответствующие валы или детали крепления; числовое слагаемое зависит от конструкции данной гитары. Однако вторая из комбинаций (10) может быть принята только в том случае, когда колесо Z2 устанавливается на первом ведущем валу и если передача z2/z3 замедляющая или не содержит большого ускорения. Желательно, чтобы z2/z3 < 1,2...1,5 и ни в коем случае не было более 2.

Например, комбинацию (33*59) : (65*71) лучше использовать в виде 59/65 * 33/71 Но в подобном же случае неприменимо соотношение 80/92 * 40/97 если колесо z = 80 не размещается на первом валу. Иногда для заполнения соответствующих интервалов передаточных отношений в таблицах даны неудобные комбинации колес, например 37/41 * 92/79 При таком порядке колес не соблюдается условие (11). Поменять местами ведущие колеса нельзя, так как колесо z = 92 не размещается на первом валу. Эти комбинации указаны для случаев, когда любыми средствами нужно получить более точное передаточное отношение. Можно также прибегнуть в этих случаях к способам уточненных настроек (стр. 401). Для ускорительных передач (i > 1) желательно так разбивать i = i1i2 чтобы сомножители были возможно более близкими один к другому и равномернее распределялось повышение скорости. При этом лучше, если i1 > i2

МИНИМАЛЬНЫЕ КОМПЛЕКТЫ СМЕННЫХ КОЛЕС

Состав комплектов сменных колес в зависимости от области применения приведен в табл. 2. В случае особо точных настроек — см. стр. 403.

Таблица 2

Числа зубьев минимальных комплектов сменных колес для различных случаев настроек

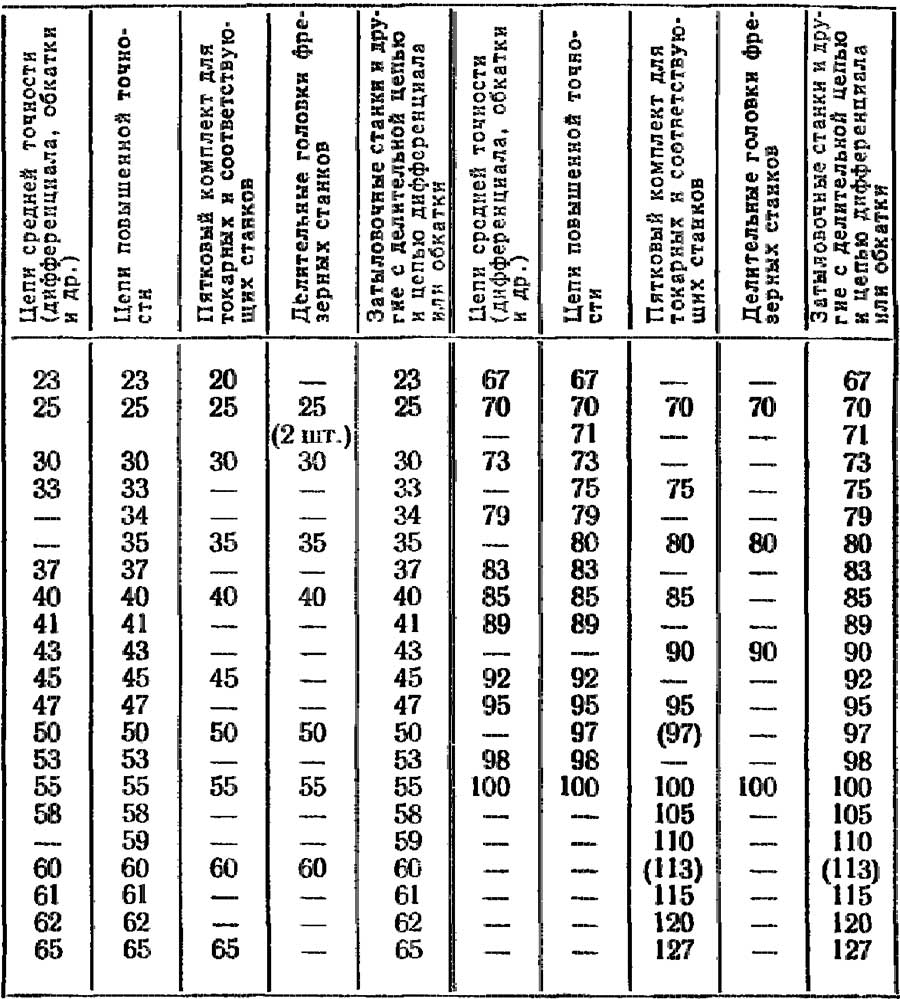
Для настройки делительных головок можно использовать таблицы, прилагаемые заводом. Сложнее, но можно выбирать подходящие пятковые комбинации из приводимых в данной книге «Основных таблиц для подбора зубчатых колес».